VARIANTE A auf Luftkissenschiene mit Lichtschranke
VARIANTE B mit wireless Smart Carts
Aufbau VARIANTE B mit wireless Smart Carts
Smart Carts schwingen gleichphasig
Smart Carts schwingen gegenphasig
VARIANTE A:
2 Gleiter zwischen 3 gleichen Spiralfedern auf der Luftkissenschiene mit Schwingungsdauer der sym. Schwingung T₁ = 3,88 s und Schwingungsdauer der antisym. Schwingung T₂ = 2,26 s
VARIANTE B:
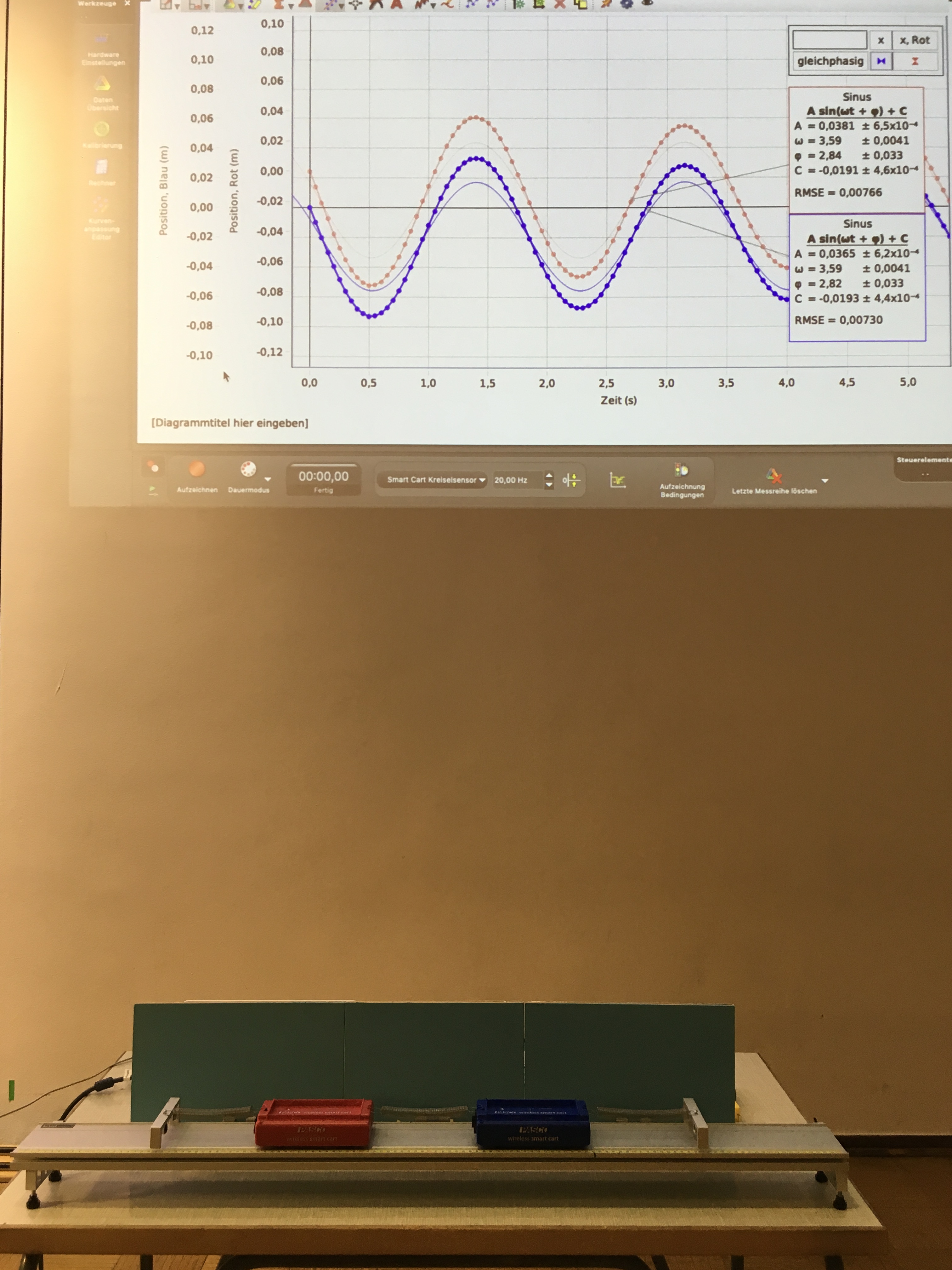
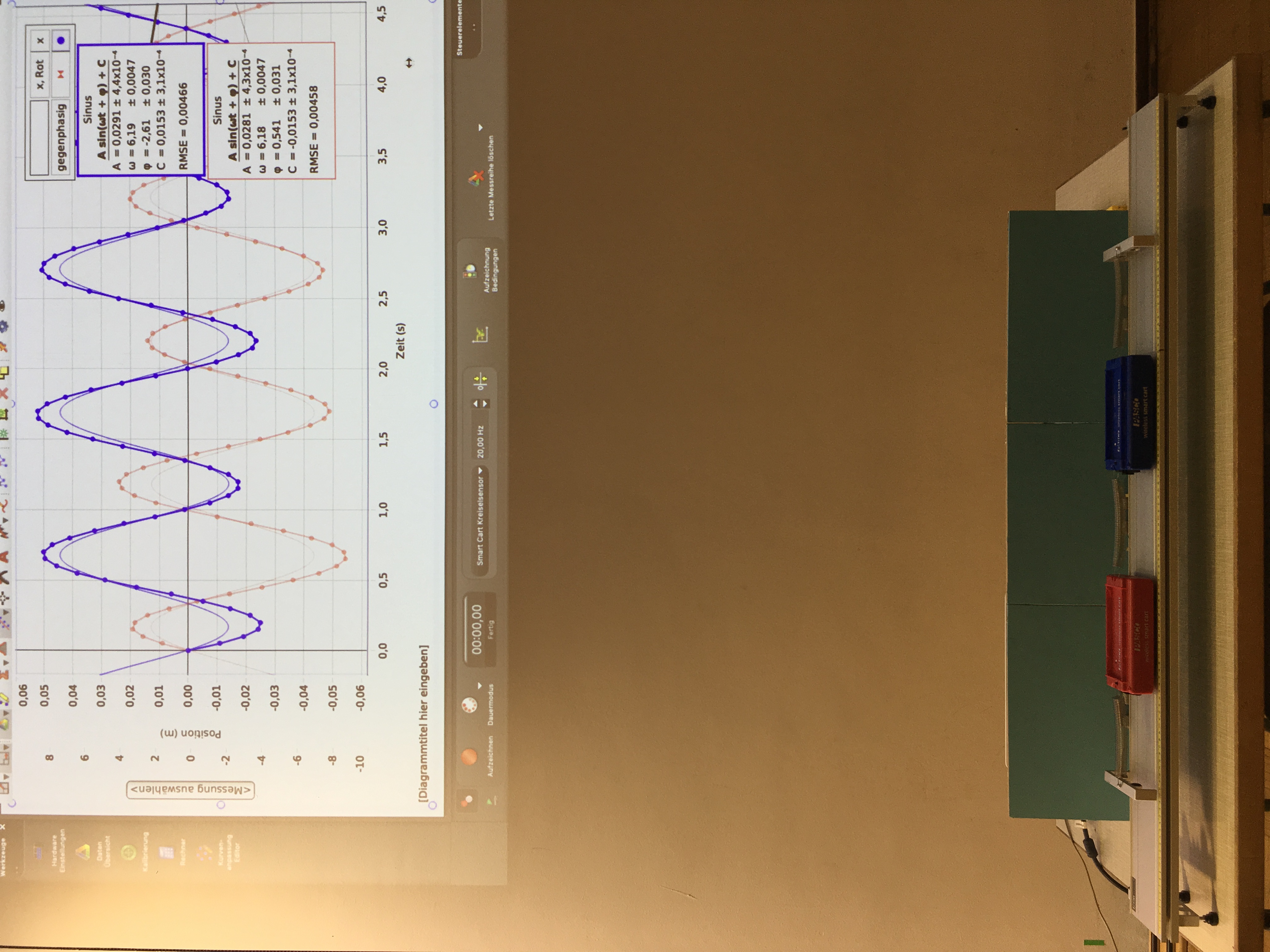
2 PASCO smart carts zwischen 3 gleichen Spiralfedern auf der Aluminiumschiene mit Schwingungsdauer der sym. Schwingung T₁ = 1,75 s und Schwingungsdauer der antisym. Schwingung T₂ = 1,02 s
Besteht eine Kette gekoppelter Pendel aus n Massen, so kann jede Masse in Longitudinalrichtung schwingen und wir erhalten n Eigenschwingungen (auch Normalschwingungen genannt) in Longitudinalrichtung.
Sind beim gekoppelten Pendel zweier Massen die Anfangsgeschwindigkeiten der beiden Massen null, so kann man durch geeignete Wahl der Anfangsauslenkungen zwei spezielle Schwingungen erzeugen. Lenkt man die beiden gleichen Massen m um die gleiche Länge in dieselbe Richtung aus, so schwingen sie anschließend in Phase. Diese symmetrische Eigenschwingung hat die Frequenz
\(\omega _{1}=\sqrt{\frac{D}{m}}\)
Lenkt man die beiden gleichen Massen m um die gleiche Länge in entgegengesetzte Richtung aus, so schwingen sie gegensinnig oder gegenphasig. Der Schwerpunkt der beiden Massen bleibt immer am selben Ort, der Relativabstand variiert. Die Kopplung wird maximal beansprucht. Diese antisymmetrische Schwingung ist die zweite Normal- oder Eigenschwingung des Systems mit der Frequenz
\(\omega _{2}=\sqrt{\frac{3D}{m}}\)
Quelle: http://www.chemgapedia.de/vsengine/
Für Chemiker ist es hilfreich darauf hinzuweisen, dass die Bezeichnungen „symmetrische“ und „antisymmetrische“ Schwingung z.B. bei 3-atomigen Molekülen wie CO2 anders ist als die Bezeichnungsweise der Physiker für gekoppelte Schwingungen von 3 Massen.
Quellen:
http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/3/anc/ir_spek/molekuelschwingungen.vlu/Page/vsc/de/ch/3/anc/ir_spek/schwspek/mol_spek/ir3_1/dreiatomlinear_m19ht0300.vscml.html
und http://www.chemgapedia.de/vsengine/vlu/vsc/de/ph/14/ep/einfuehrung/schwingungen/gekoppelt/gekoppelt.vlu/Page/vsc/de/ph/14/ep/einfuehrung/schwingungen/gekoppelt/gek_freiheitsgrade.vscml.html
2 Gleiter zwischen 3 gleichen Spiralfedern auf der Luftkissenschiene mit Schwingungsdauer der sym. Schwingung T₁ = 3,88 s und Schwingungsdauer der antisym. Schwingung T₂ = 2,26 s
VARIANTE B:
2 PASCO smart carts zwischen 3 gleichen Spiralfedern auf der Aluminiumschiene mit Schwingungsdauer der sym. Schwingung T₁ = 1,75 s und Schwingungsdauer der antisym. Schwingung T₂ = 1,02 s
Besteht eine Kette gekoppelter Pendel aus n Massen, so kann jede Masse in Longitudinalrichtung schwingen und wir erhalten n Eigenschwingungen (auch Normalschwingungen genannt) in Longitudinalrichtung.
Sind beim gekoppelten Pendel zweier Massen die Anfangsgeschwindigkeiten der beiden Massen null, so kann man durch geeignete Wahl der Anfangsauslenkungen zwei spezielle Schwingungen erzeugen. Lenkt man die beiden gleichen Massen m um die gleiche Länge in dieselbe Richtung aus, so schwingen sie anschließend in Phase. Diese symmetrische Eigenschwingung hat die Frequenz
\(\omega _{1}=\sqrt{\frac{D}{m}}\)
Lenkt man die beiden gleichen Massen m um die gleiche Länge in entgegengesetzte Richtung aus, so schwingen sie gegensinnig oder gegenphasig. Der Schwerpunkt der beiden Massen bleibt immer am selben Ort, der Relativabstand variiert. Die Kopplung wird maximal beansprucht. Diese antisymmetrische Schwingung ist die zweite Normal- oder Eigenschwingung des Systems mit der Frequenz
\(\omega _{2}=\sqrt{\frac{3D}{m}}\)
Quelle: http://www.chemgapedia.de/vsengine/
Für Chemiker ist es hilfreich darauf hinzuweisen, dass die Bezeichnungen „symmetrische“ und „antisymmetrische“ Schwingung z.B. bei 3-atomigen Molekülen wie CO2 anders ist als die Bezeichnungsweise der Physiker für gekoppelte Schwingungen von 3 Massen.
Quellen:
http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/3/anc/ir_spek/molekuelschwingungen.vlu/Page/vsc/de/ch/3/anc/ir_spek/schwspek/mol_spek/ir3_1/dreiatomlinear_m19ht0300.vscml.html
und http://www.chemgapedia.de/vsengine/vlu/vsc/de/ph/14/ep/einfuehrung/schwingungen/gekoppelt/gekoppelt.vlu/Page/vsc/de/ph/14/ep/einfuehrung/schwingungen/gekoppelt/gek_freiheitsgrade.vscml.html