\(M=Konst.\cdot T^{4}\)
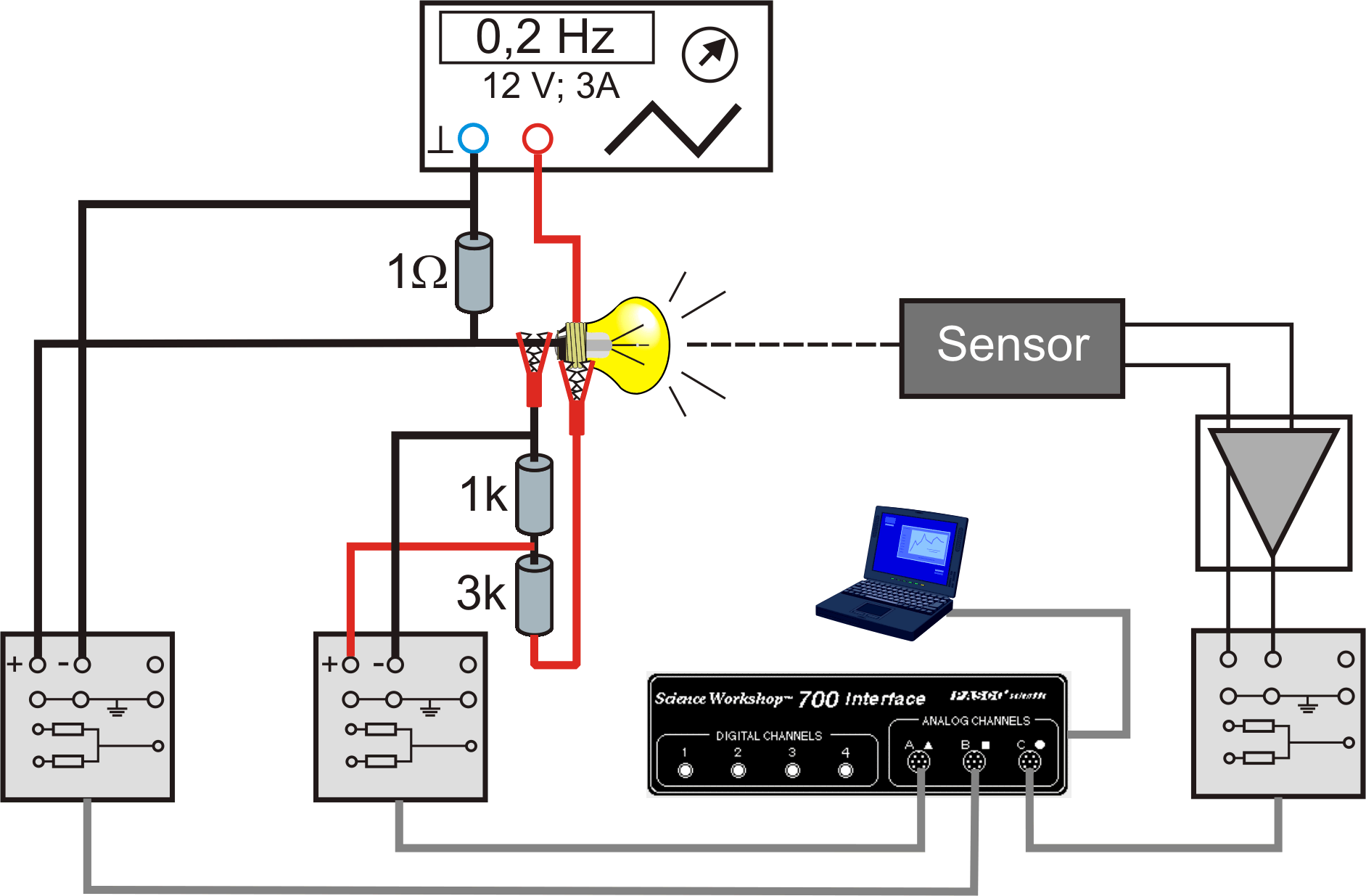
Untersucht wird die Strahlung einer Wolframwendel (Autoglühlampe).
Mit einem Strahlungsempfänger wird die Strahlungsleistung M der Glühwendel gemessen.
Neuere Fassung siehe O.F.2.3
Josef Stefan (St. Peter 1835 - Wien 1893): Experimentelle Entdeckung
Ludwig Erhard Boltzmann (Wien 1844 - Triest 1906): Theoretische Herleitung
Die Temperatur T der Glühwendel wird berechnet aus \(T=T_{ref}+\frac{R-R_{ref}}{a\cdot R_{ref}}\).
Dabei ist R der Widerstand der Wendel, den man durch Spannungs- und Strom-Messung an der Glühwendel bestimmt. In einem Vorversuch wurde \(R_{ref}=0,315\:\Omega \) bei \(T_{ref}=295,2\:\text{K} \) ermittelt.
Aus \(R(T)=R(295\:\text{K})\cdot (1+a\cdot (T-295\:\text{K}))\) erhält man mit \(a=4,5\cdot 10^{-3}\text{K}^{-1}\) (Steigung der Funktion R(T)):
\(T=(705,5\frac{\text{K}}{\Omega }\cdot R+73,0\:\text{K})\)
Mit Laptop und automatischer Messwerterfassung wird M über T sowie M über \(T^{4}\) dargestellt (letzteres ergibt eine Gerade).
Geräteliste wurde nur für diesen Aufbau erstellt, ebenso Skizze und Bild.
Wichtig: Lampe nur mit max. 12 V belastbar!!!
Alter Versuch mit Auswertungsprinzip:
Tabelle (für alte Auswertung):
Messreihe 1. 2. 3. 4. 5.
einstellen: U / V 2,0 4,4 6,0 8,0 10,0
ablesen: I / A
berechnen: \(R\, /\, \Omega \)
berechnen: T / K
ablesen: M / mV
berechnen: log T
berechnen: log M
Diagramm: log M als Funktion von log T auftragen. Die Steigung der Geraden sollte den Exponenten 4 ergeben. (Maßstab für eine Dekade auf der x-/y-Achse berücksichtigen!)
Identisch mit W.D.9.5
Untersucht wird die Strahlung einer Wolframwendel (Autoglühlampe).
Mit einem Strahlungsempfänger wird die Strahlungsleistung M der Glühwendel gemessen.
Neuere Fassung siehe O.F.2.3
Josef Stefan (St. Peter 1835 - Wien 1893): Experimentelle Entdeckung
Ludwig Erhard Boltzmann (Wien 1844 - Triest 1906): Theoretische Herleitung
Die Temperatur T der Glühwendel wird berechnet aus \(T=T_{ref}+\frac{R-R_{ref}}{a\cdot R_{ref}}\).
Dabei ist R der Widerstand der Wendel, den man durch Spannungs- und Strom-Messung an der Glühwendel bestimmt. In einem Vorversuch wurde \(R_{ref}=0,315\:\Omega \) bei \(T_{ref}=295,2\:\text{K} \) ermittelt.
Aus \(R(T)=R(295\:\text{K})\cdot (1+a\cdot (T-295\:\text{K}))\) erhält man mit \(a=4,5\cdot 10^{-3}\text{K}^{-1}\) (Steigung der Funktion R(T)):
\(T=(705,5\frac{\text{K}}{\Omega }\cdot R+73,0\:\text{K})\)
Mit Laptop und automatischer Messwerterfassung wird M über T sowie M über \(T^{4}\) dargestellt (letzteres ergibt eine Gerade).
Geräteliste wurde nur für diesen Aufbau erstellt, ebenso Skizze und Bild.
Wichtig: Lampe nur mit max. 12 V belastbar!!!
Alter Versuch mit Auswertungsprinzip:
Tabelle (für alte Auswertung):
Messreihe 1. 2. 3. 4. 5.
einstellen: U / V 2,0 4,4 6,0 8,0 10,0
ablesen: I / A
berechnen: \(R\, /\, \Omega \)
berechnen: T / K
ablesen: M / mV
berechnen: log T
berechnen: log M
Diagramm: log M als Funktion von log T auftragen. Die Steigung der Geraden sollte den Exponenten 4 ergeben. (Maßstab für eine Dekade auf der x-/y-Achse berücksichtigen!)
Identisch mit W.D.9.5
Vorbereitung
2d